Longest Common Subsequence

Now, we will look through how to solve a popular dynamic programming problem,

LCS or longest common subsequence problem.

Problem Statement : Given two sequences, find the length of longest subsequence present in both of them. A subsequence is a sequence that appears in the same relative order, but not necessarily contiguous.

Example :   LCS for input Sequences “ABCDGH” and “AEDFHR” is “ADH” of length 3.

                       LCS for input Sequences “AGGTAB” and “GXTXAYB” is “GTAB” of length 4.

Solution :   First of all lets see how to approach the problem and see how this problem qualifies to be a DP problem. 

1) Optimal Substructure:
Let the input sequences be X[0..m-1] and Y[0..n-1] of lengths m and n respectively. And let L(X[0..m-1], Y[0..n-1]) be the length of LCS of the two sequences X and Y. Following is the recursive definition of L(X[0..m-1], Y[0..n-1]).

If last characters of both sequences match (or X[m-1] == Y[n-1]) then
L(X[0..m-1], Y[0..n-1]) = 1 + L(X[0..m-2], Y[0..n-2])

If last characters of both sequences do not match (or X[m-1] != Y[n-1]) then
L(X[0..m-1], Y[0..n-1]) = MAX ( L(X[0..m-2], Y[0..n-1]), L(X[0..m-1], Y[0..n-2]) )

Examples:
1) Consider the input strings “AGGTAB” and “GXTXAYB”. Last characters match for the strings. So length of LCS can be written as:
L(“AGGTAB”, “GXTXAYB”) = 1 + L(“AGGTA”, “GXTXAY”)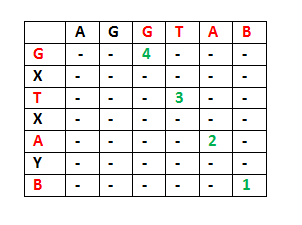

2) Consider the input strings “ABCDGH” and “AEDFHR. Last characters do not match for the strings. So length of LCS can be written as:
L(“ABCDGH”, “AEDFHR”) = MAX ( L(“ABCDG”, “AEDFHR”), L(“ABCDGH”, “AEDFH”) )

So the LCS problem has optimal substructure property as the main problem can be solved using solutions to subproblems.

2) Overlapping Subproblems:
Following is simple recursive implementation of the LCS problem. The implementation simply follows the recursive structure mentioned above.

/* A Naive recursive implementation of LCS problem */
#include <bits/stdc++.h> 
using namespace std; 

int max(int a, int b); 

/* Returns length of LCS for X[0..m-1], Y[0..n-1] */
int lcs( char *X, char *Y, int m, int n ) 
{ 
	if (m == 0 || n == 0) 
		return 0; 
	if (X[m-1] == Y[n-1]) 
		return 1 + lcs(X, Y, m-1, n-1); 
	else
		return max(lcs(X, Y, m, n-1), lcs(X, Y, m-1, n)); 
} 

/* Utility function to get max of 2 integers */
int max(int a, int b) 
{ 
	return (a > b)? a : b; 
} 

/* Driver code */
int main() 
{ 
	char X[] = "AGGTAB"; 
	char Y[] = "GXTXAYB"; 
	
	int m = strlen(X); 
	int n = strlen(Y); 
	
	cout<<"Length of LCS is "<< lcs( X, Y, m, n ) ; 
	
	return 0; 
}